Cross-diffusion in population dynamics
PSC (Collective Scientific Project) at Ecole Polytechnique
This project was conducted under the supervision of Vincent Bansaye and Maxime Breden from Polytechnique’s CMAP.
Acces to report :
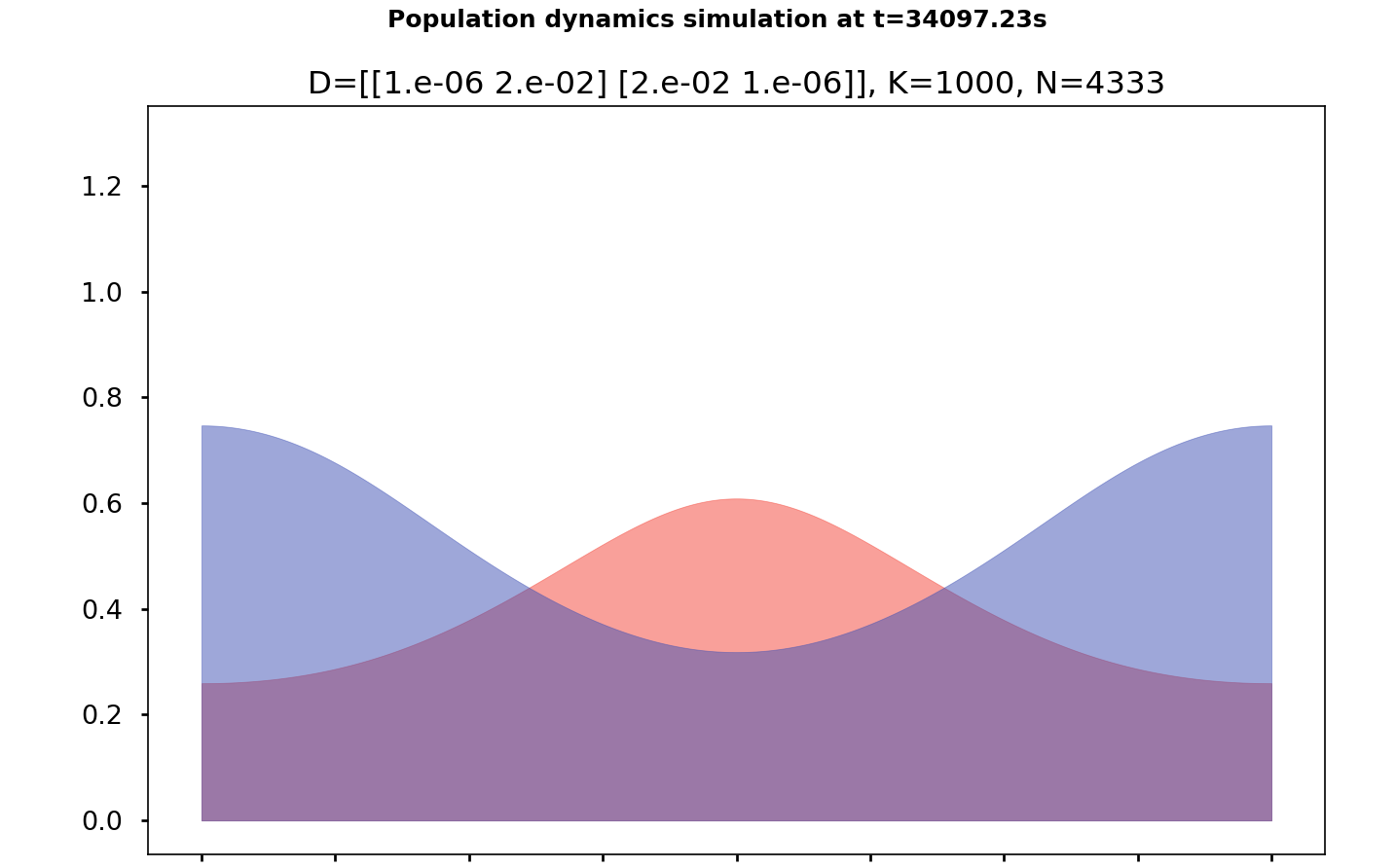
In population dynamics, cross-diffusion reveals local interactions that lead to spatial segregation between two species. To describe these repulsive effects, we first develop a probabilistic model that also considers birth and death events, simulated using the Gillespie algorithm. This approach naturally leads, in the limit, to a deterministic behavior described by a system of partial differential equations. Due to the presence of a nonlinear cross-diffusion term in the initial system, solving it numerically is challenging, especially over long time periods.
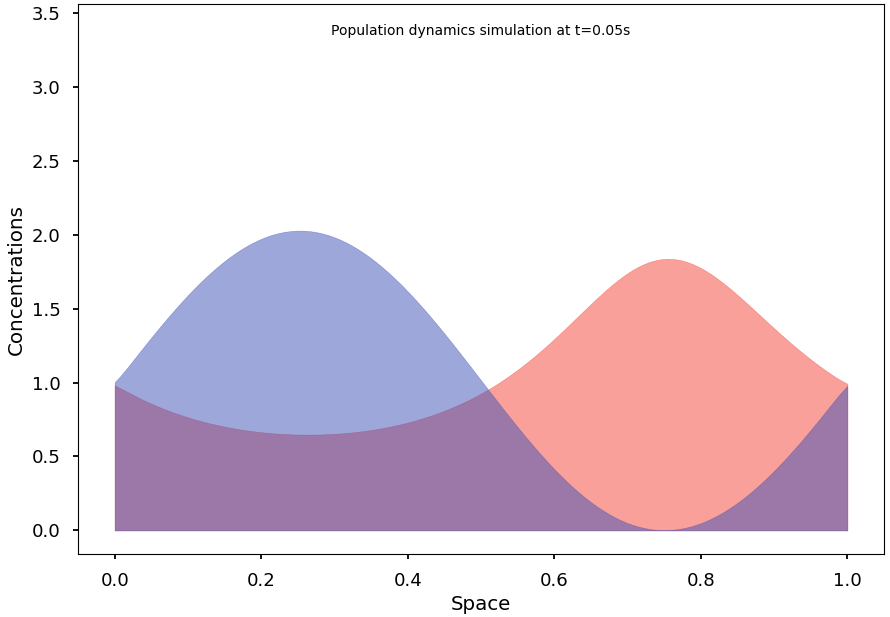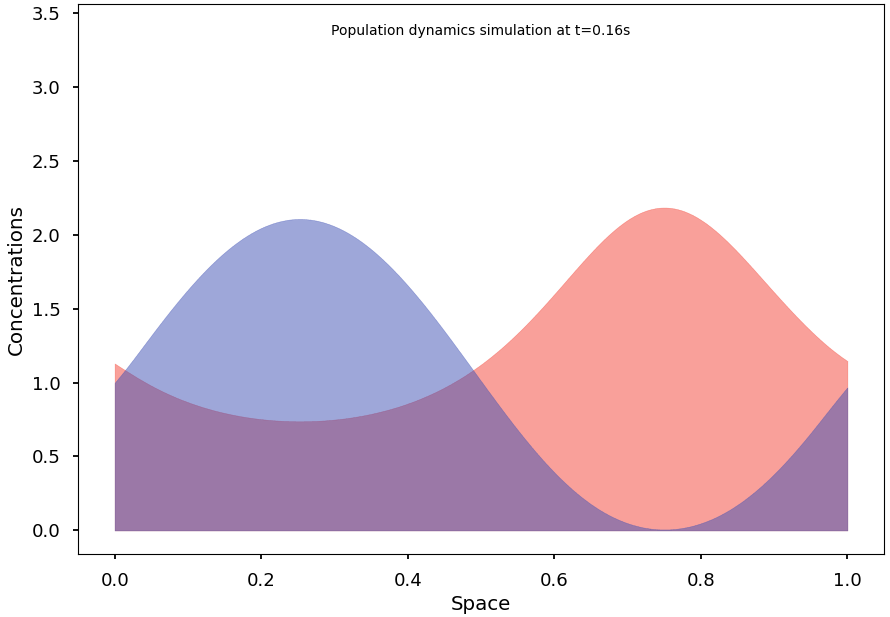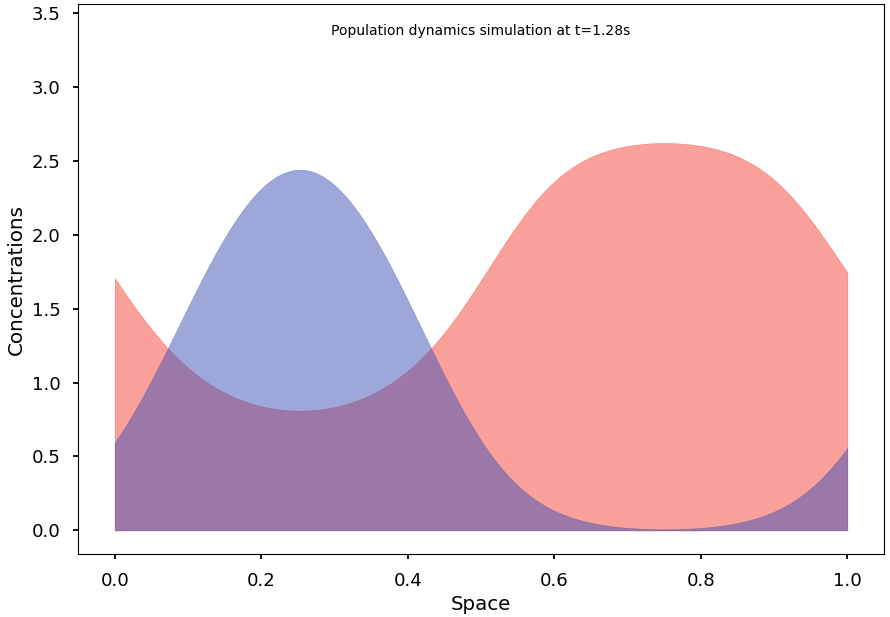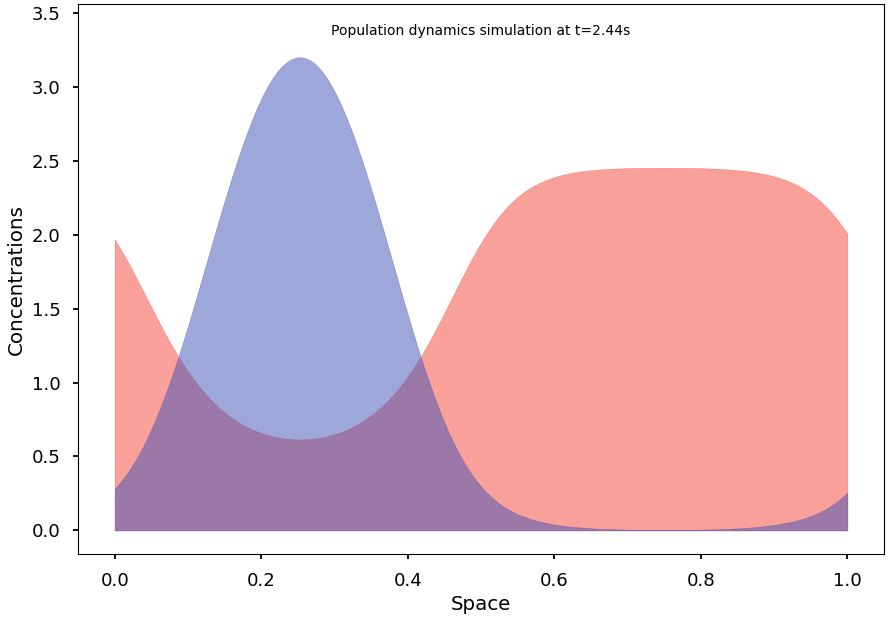
To reach and observe the system’s stationary states, we subsequently implement an efficient integration algorithm for the continuous model. We then formulate some conjectures on conditions that may promote segregation at equilibrium and demonstrate initial results in this regard.
Finally, we explain and illustrate how, and to what extent, the continuous model can indeed be understood as the natural limit of the stochastic Markov process.
Stochastic implementation
In this section, we simulate this deterministic evolution using a probabilistic approach and will later demonstrate how these two models are connected. We work within a space containing an integer number of individuals of each species distributed across MM discrete sites. Three types of events can occur: an individual moving from one site to an adjacent site, the birth of an individual, or the death of an individual. The probability of each event occurring within a given time interval depends on the concentration of each species and their coexistence, following a scheme similar to the SKT model equation, which we will detail in the final section. These events influence the overall population distribution and occur after a certain reaction time.
Each individual remains at a site for a random period, determined by an exponential distribution with an average inversely proportional to the number of individuals at that site. If an individual moves, the destination site is chosen uniformly from adjacent sites. The model then evolves after the reaction time of the individual that reacts first, resetting the reaction times for all other individuals according to the new distribution. This initial reaction time can thus be regarded as the general jump time of the given distribution.
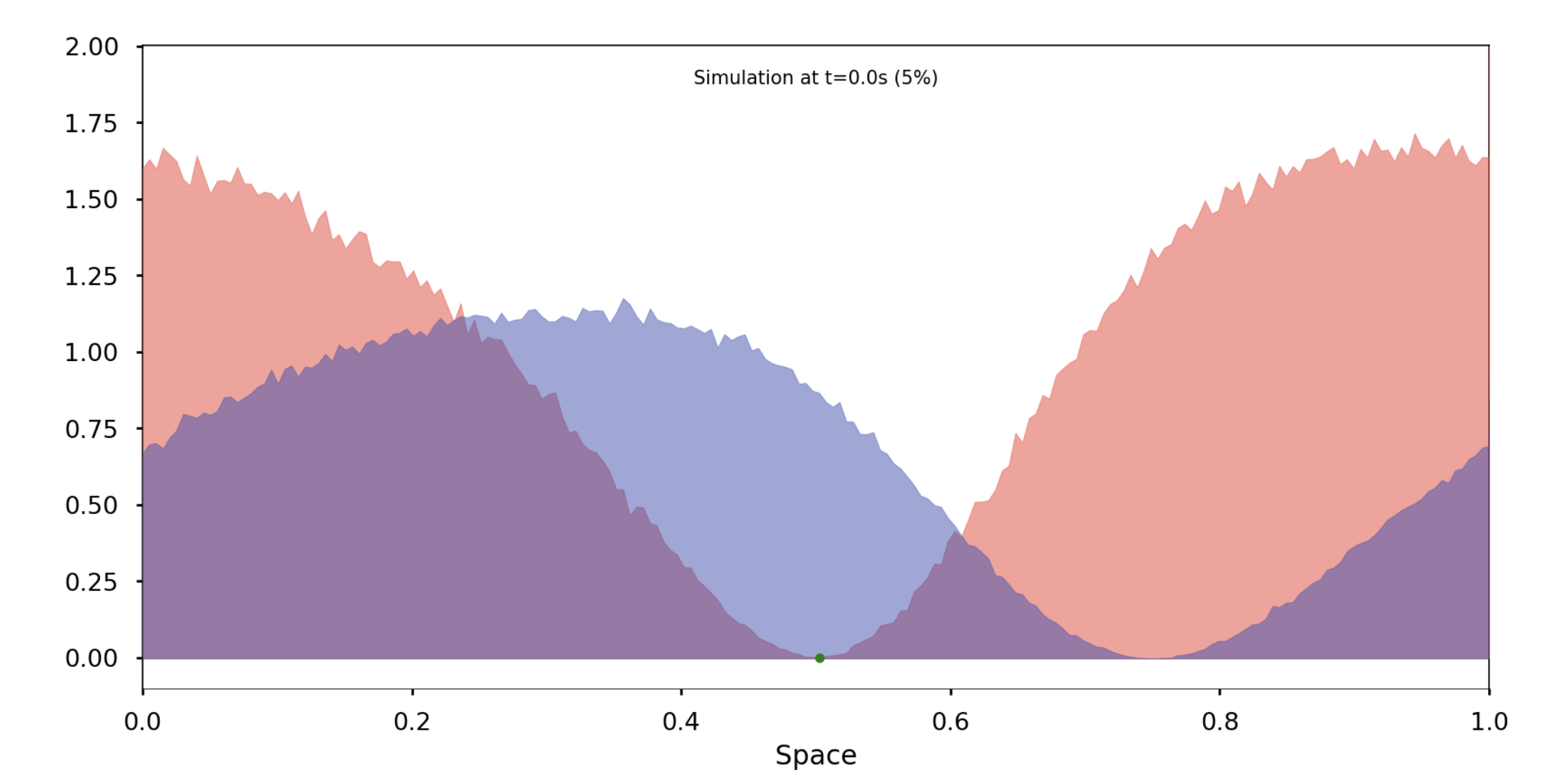
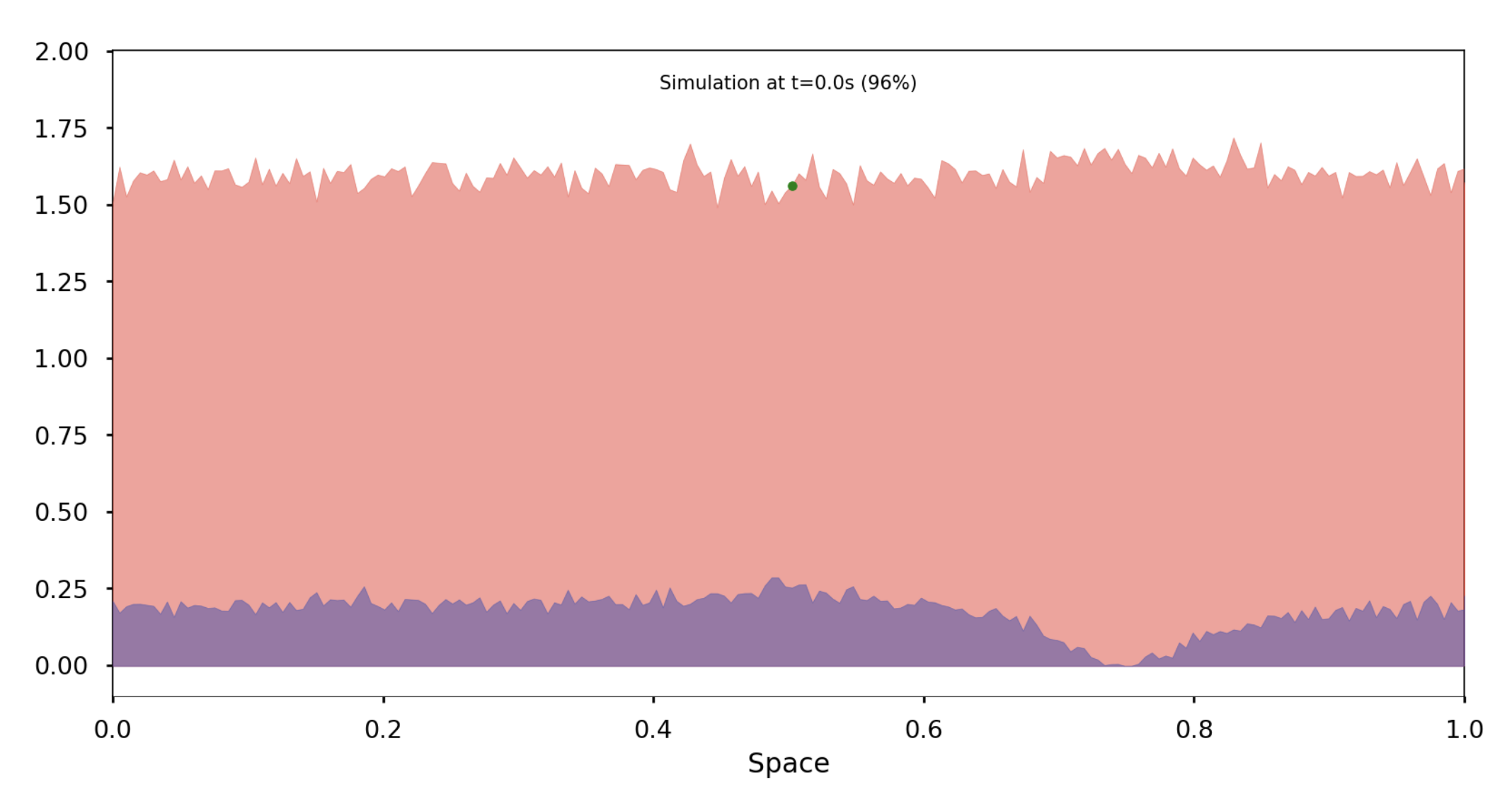
Deterministic implementation
SKT Model proposed by Sheguesada, Kawazaki et Teramoto :
\[\begin{cases} \partial_{t}u-\Delta\left(d_{1}u+d_{11}u^{2}+d_{12}uv\right) & =u\left(r_{1}-a_{1}u-b_{1}v\right)\\ \partial_{t}v-\Delta\left(d_{2}v+d_{21}uv+d_{22}v^{2}\right) & =v\left(r_{2}-b_{2}u-a_{2}v\right) \end{cases}\qquad\text{sur}\,[0,1]\times\mathbb{R}_{+}.\]where \(u(x,t)\) et \(v(x,t)\) are concentrations (positive) of the 2 species. Coefficients are gathered in the diffision matrix \(\mathcal{D}\) and the reaction matrix \(\mathcal{R}\) :
\[\mathcal{D}:=\begin{pmatrix}d_{1} & d_{11} & d_{12}\\ d_{2} & d_{21} & d_{22} \end{pmatrix}\qquad\text{et}\qquad\mathcal{R}:=\begin{pmatrix}r_{1} & a_{1} & b_{1}\\ r_{2} & b_{2} & a_{2} \end{pmatrix}\]The prey-predator system of Lotka-Volterra is : \(\mathcal{D}:=\textbf{0}_{2\times3}\quad\text{et}\quad\mathcal{R}:=\begin{pmatrix}a & 0 & b\\ -d & -c & 0 \end{pmatrix}.\)
We operate under periodic boundary conditions, but the results we present can also be extended to homogeneous Neumann boundary conditions.
It can be shown, under certain conditions, that the semi-continuous model is the deterministic limit of the stochastic framework previously described. We quickly developed a library to solve this class of systems to:
- Experimentally understand the roles of various parameters;
- Quantify the difference between the two models, and even the rate of convergence.
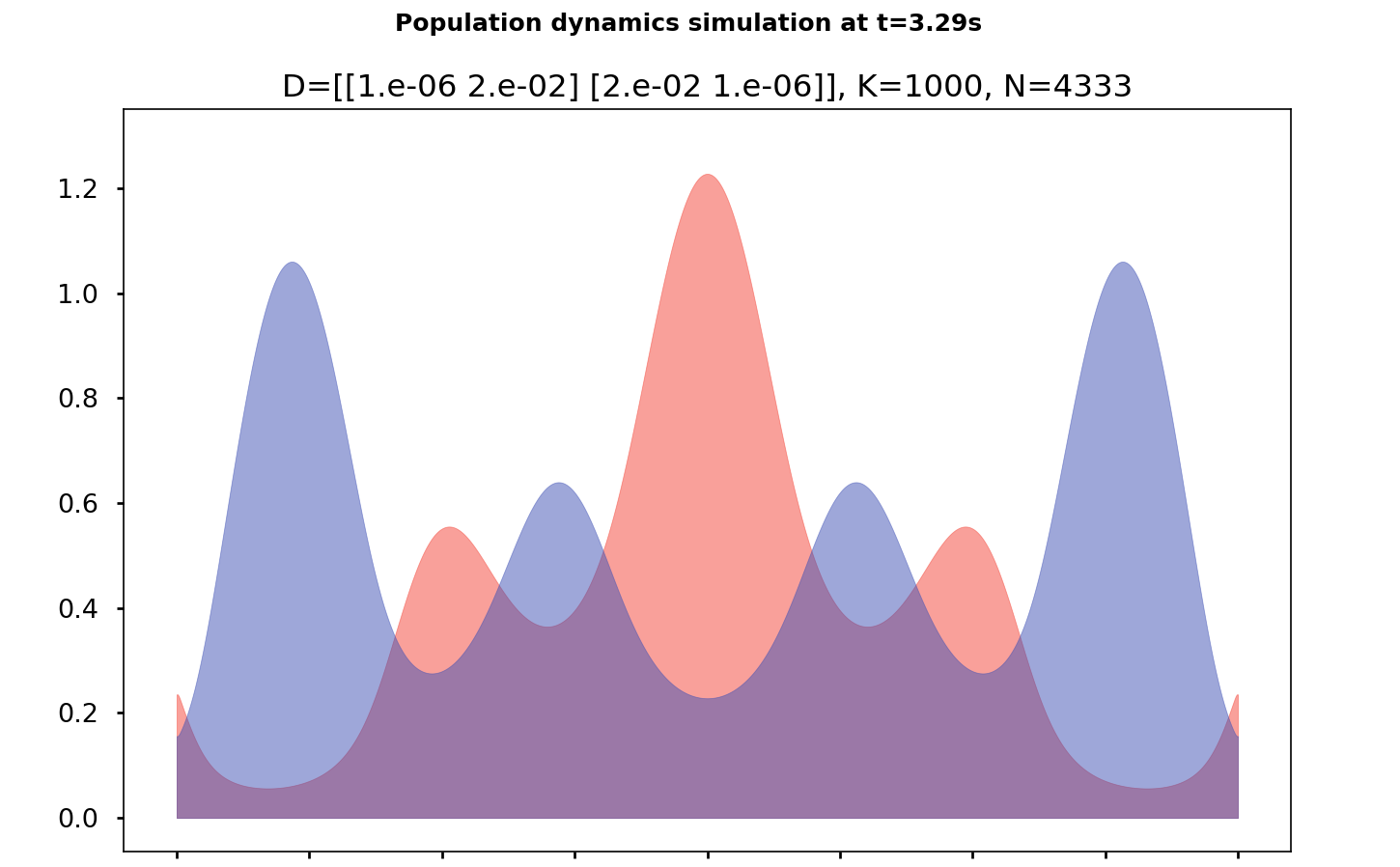
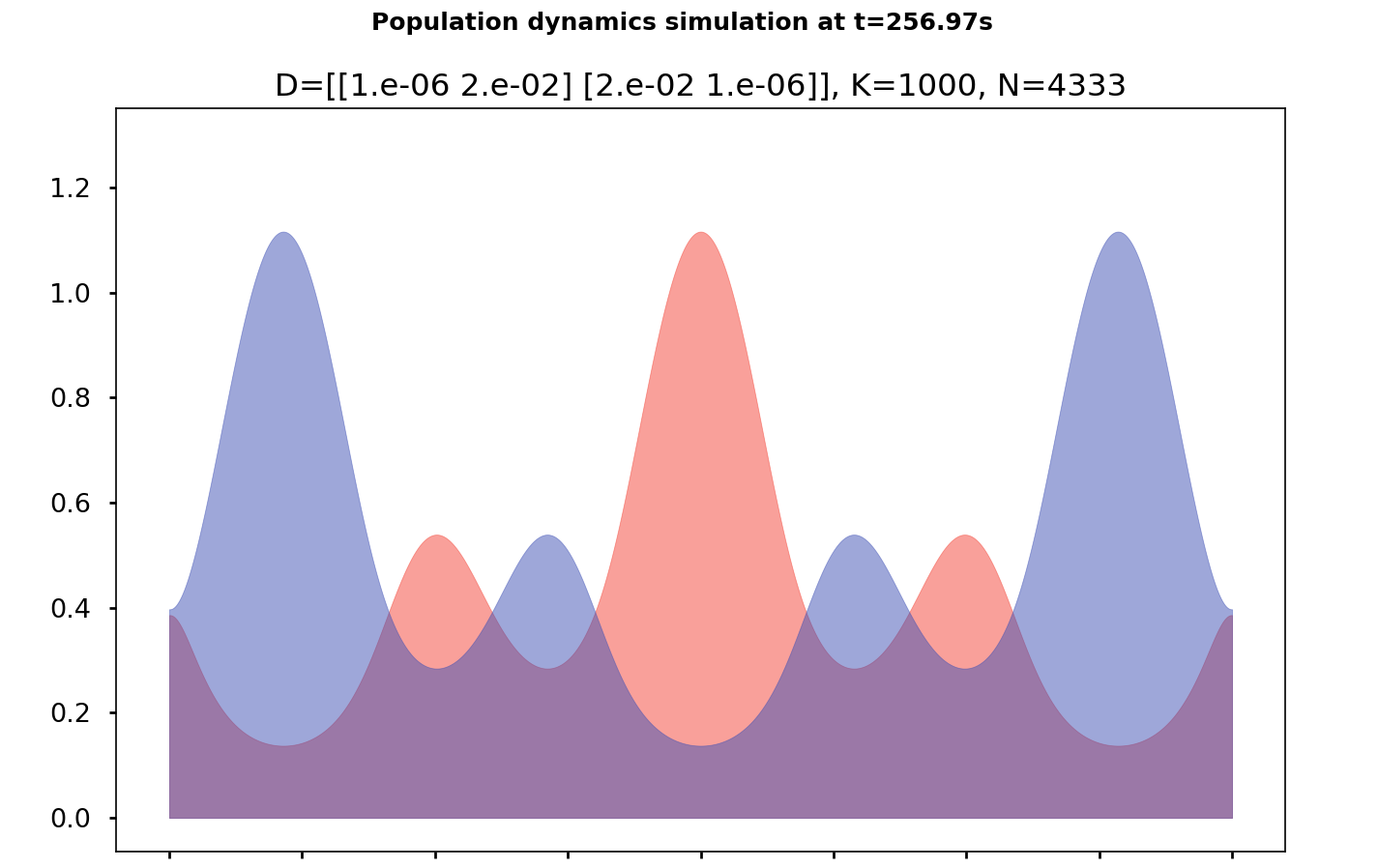
The library is available at PySpecies