Championship Modeling, Simulating Football Outcomes
MODAL, Random numerical simulation (SNA) of rare events
This project was conducted under the supervision of Professor Gersende Fort from Polytechnique.
Acces to report :
Analysis of Rare Event Simulation in Sports Betting
In the sports betting industry, bookmakers rely on extensive digital and statistical tools to evaluate the odds for each team’s victory. One striking example of a rare outcome in football history is Leicester City’s unexpected win in the 2015-2016 Premier League season, which defied all predictions. Inspired by this season, we developed a model to simulate rare events in a tournament setting, which we tested and analyzed against real data.
Overview of Content:
- Problem Definition
- Initial Estimations
- Preferential Sampling
- Splitting Method
- Discussion of Assumptions
Problem Definition
Our model uses the Bradley-Terry framework, a popular approach for modeling competitive tournaments. Here, each team ii has an intrinsic value ViVi, determining its probability $pij:=Vi/(Vi+Vj)pij:=Vi/(Vi+Vj)$ of winning against any opponent jj. Using this probability framework, we constructed a 20-team tournament matrix and simulated head-to-head matches to build a probability matrix of match outcomes.
Initial Estimations
Our first step was to implement a Monte Carlo simulation with 100,000 tournaments to estimate the win probability for each team. Comparing our results with bookmakers’ predictions, we found that while our model reasonably matched bookmaker estimates for top teams, it struggled to accurately reflect outcomes for weaker teams, such as Leicester. Here, the Monte Carlo method alone was inadequate for capturing these rare event probabilities.
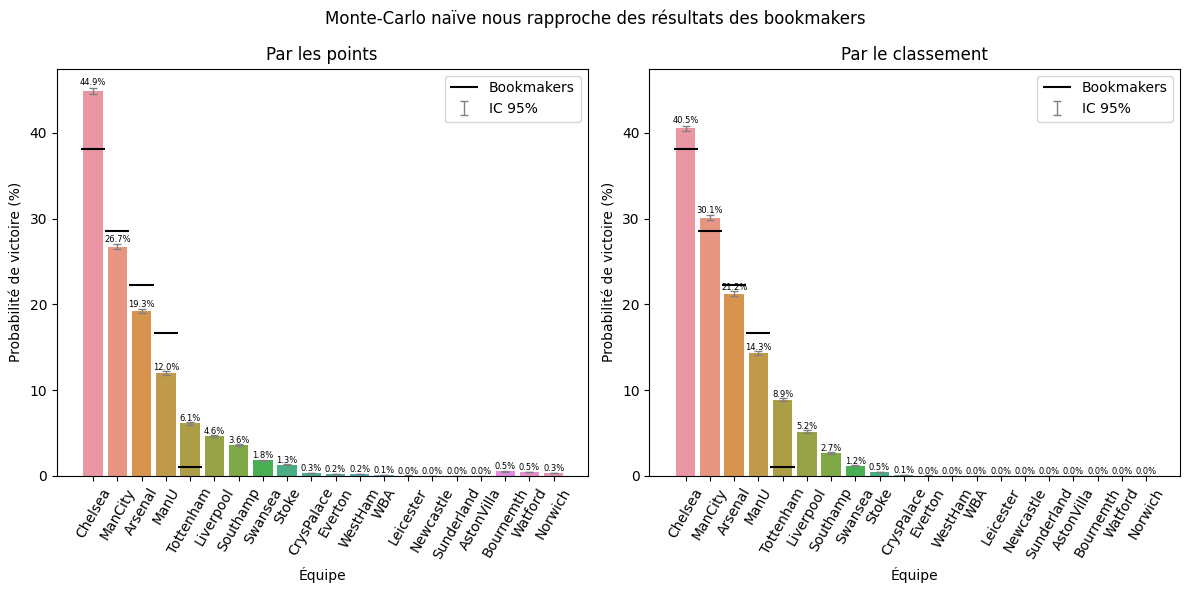
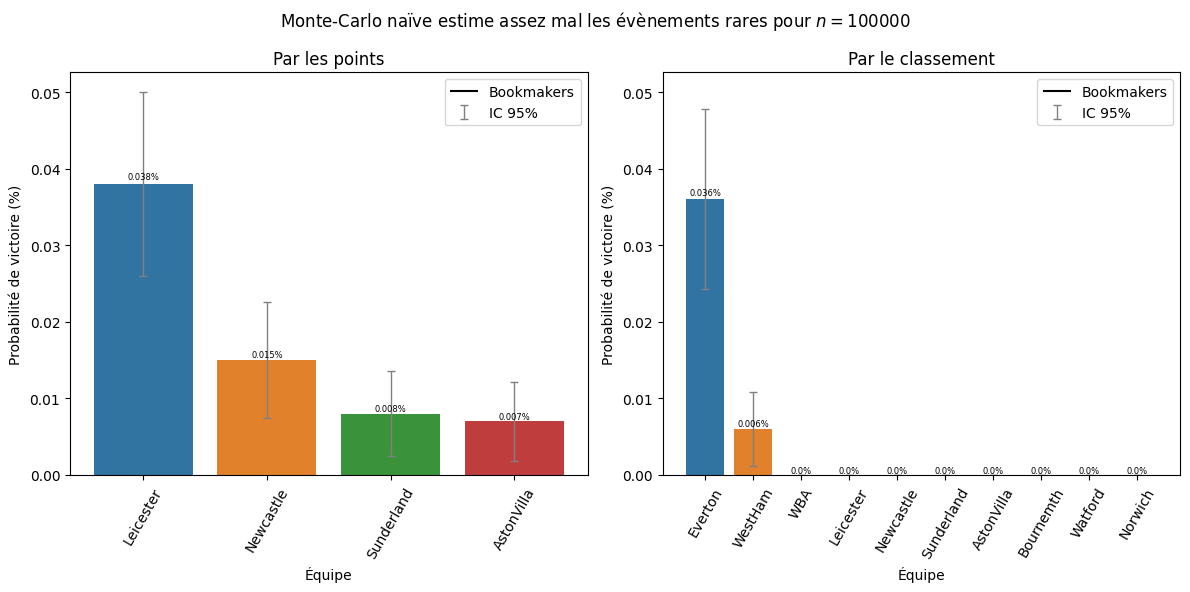
Preferential Sampling
To address the limitations of the Monte Carlo method for low-probability events, we implemented importance sampling. By adjusting the intrinsic values within the model to make a Leicester win more likely, we reduced the computational effort by a factor of 100, achieving an error margin of around 3% with far fewer simulations. We found that setting Leicester’s strength near Chelsea’s (the top team) yielded the most stable error estimates, confirming that higher values improved our simulation’s accuracy.
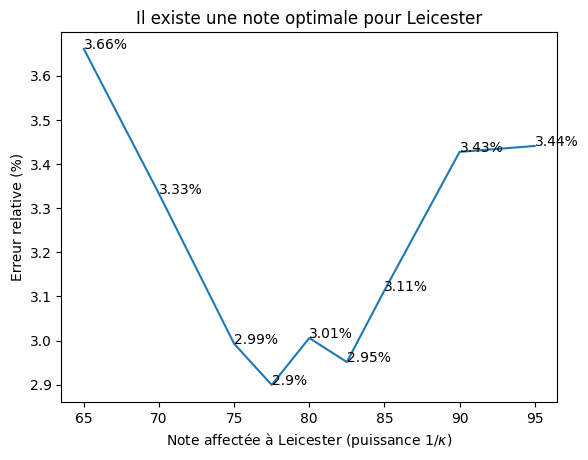
Splitting Method
As a second approach, we used a “splitting” method, which progressively adjusted Leicester’s scores in multiple stages to increase their probability of winning in the simulations. This method provided a practical alternative to naive Monte Carlo but was still limited when Leicester’s overall win probability was less than 1%, a threshold where our computations required extensive adjustments to remain effective.
Discussion of Assumptions
Our assumptions included treating teams as equal winners if they had identical scores, running two-match rounds for each pair, and assuming constant intrinsic values. We tested variations of these assumptions to see their impact:
Tie-breaking Rules: When selecting a winner from tied teams, weaker teams like Leicester were further disadvantaged if we broke ties in favor of the highest-rated team.
Impact of Repeated Matches: Increasing the number of encounters between teams resulted in a higher likelihood that the best-rated team (Chelsea) would win, due to a cumulative advantage over repeated games.
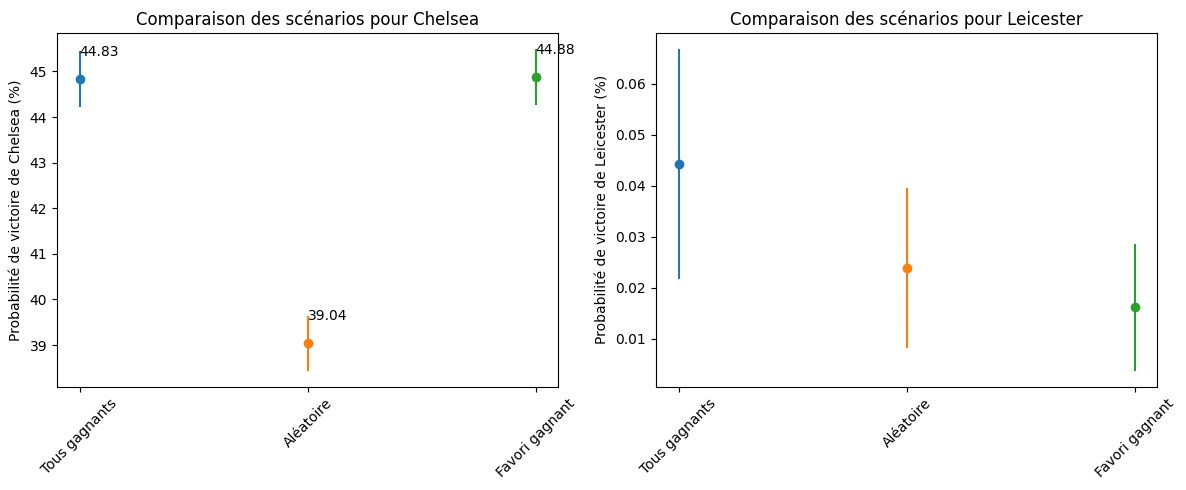
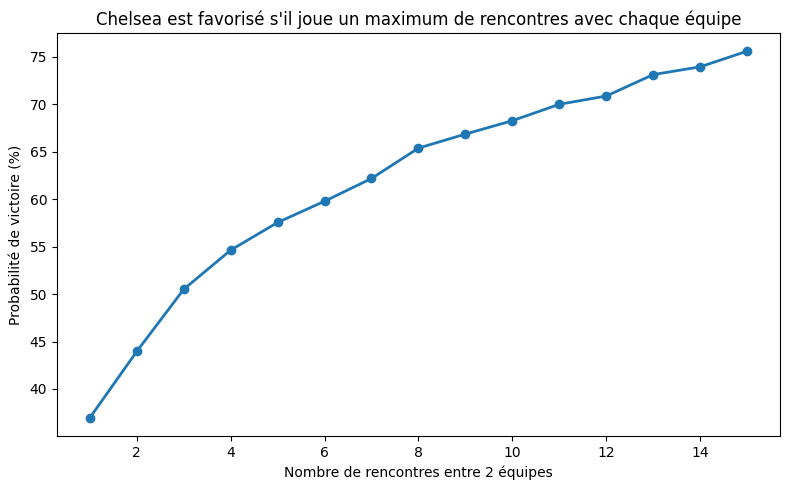
Towards a Realistic Model
Future improvements could involve accounting for additional match factors, like home vs. away advantage, the influence of consecutive wins, and a point system that mirrors real leagues. These modifications could better align our model’s win probabilities with bookmaker predictions.
Conclusion
Through this project, we explored several techniques for modeling rare outcomes in sports tournaments. Preferential sampling proved to be both efficient and effective in capturing the probability of rare events, while the splitting method provided additional insights into the practicalities of simulating unlikely victories in tournaments. With further refinements, we believe these methods could offer valuable tools for understanding and predicting unusual outcomes in competitive sports.